INSERTION SORT Algorithm
If the first few objects are already sorted, an unsorted object can be inserted in the sorted set in proper place. This is called insertion sort. An algorithm consider the elements one at a time, inserting each in its suitable place among those already considered (keeping them sorted). Insertion sort is an example of an incremental algorithm; it builds the sorted sequence one number at a time. This is perhaps the simplest example of the incremental insertion technique, where we build up a complicated structure on n items by first building it on n − 1 items and then making the necessary changes to fix things in adding the last item. The given sequences are typically stored in arrays. We also refer the numbers as keys. Along with each key may be additional information, known as satellite data.
Algorithm:
It works the way you might sort a hand of playing cards:
1. We start with an empty left hand [sorted array] and the cards face down on the table [unsorted array].
2. Then remove one card [key] at a time from the table [unsorted array], and insert it into the correct position in the left hand [sorted array].
3. To find the correct position for the card, we compare it with each of the cards already in the hand, from right to left.
Note that at all times, the cards held in the left hand are sorted, and these cards were originally the top cards of the pile on the table.
Idea:
Let a0, ..., an-1 be the sequence to be sorted. At the beginning and after each iteration of the algorithm the sequence consists of two parts: the first part a0, ..., ai-1 is already sorted, the second part ai, ..., an-1 is still unsorted (i  0, ..., n).
0, ..., n).
In order to insert element ai into the sorted part, it is compared with ai-1, ai-2 etc. When an element aj with aj ai is found, ai is inserted behind it. If no such element is found, then ai is inserted at the beginning of the sequence.
ai is found, ai is inserted behind it. If no such element is found, then ai is inserted at the beginning of the sequence.
After inserting element ai the length of the sorted part has increased by one. In the next iteration, ai+1 is inserted into the sorted part etc. While at the beginning the sorted part consists of element a0 only, at the end it consists of all elements a0, ..., an-1.
Example:
References:
QUICKSORT Algorithm
Quicksort is one of the fastest and simplest sorting algorithms [Hoa 62]. It works recursively by a divide-and-conquer strategy.
Like Insertion Sort, this algorithm has a fairly simple concept at the core, but is made complicated by the constraints of the array structure.
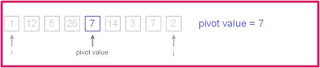
Quicksort starts by randomly picking a number called pivot.
Then rearranges the other numbers by comparing them with the pivot by this condition:
The other elements starting from the first onwards would be the i.
The other elements starting from the last backwards would be the j.
As the condition i≥pivot is not satisfied, the i will continue to increment. At the moment the condition was satisfied, the condition pivot≥j must be satisfied next.
Until the condition pivot≥j is not satisfied, j will continue to decrement and at the moment the condition was satisfied, swap i and j.
This routine will continue until i>j.
wOoooOohHh!!!
kaka nose bleed yOn ahH!
oH. .wag exited dahil partition part pa lang yon.
kaka nose bleed yOn ahH!
oH. .wag exited dahil partition part pa lang yon.
Next jan ay eto. . .
The present order of the set of numbers ay mahahati sa dalawa.
Yung group ng numbers sa left side ay lahat nung dinaanan ni i at yung group ng numbers sa right side ay lahat naman nung dinaanan ni j.
Ngayon, magkakaroon ulit ng Quicksort tulad nung nangyari dun sa partition part dun sa dalawang group of numbers until. . sa wakas ay sorted na ung set of given numbers.
GETS? Haaaaaaayst. Sana naman na gets ,nyo na dahil yan na ang dabestssssss paliwanag ever na I think maiintindihan mo. . J
Heto ang C++ code and Java ng Quicksort Algorithm.
Java
int partition(int arr[], int left, int right)
{
int i = left, j = right;
int tmp;
int pivot = arr[(left + right) / 2];
while (i <= j) {
while (arr[i] < pivot)
i++;
while (arr[j] > pivot)
j--;
if (i <= j) {
tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
i++;
j--;
}
};
return i;
}
void quickSort(int arr[], int left, int right) {
int index = partition(arr, left, right);
if (left < index - 1)
quickSort(arr, left, index - 1);
if (index < right)
quickSort(arr, index, right);
}
C++
void quickSort(int arr[], int left, int right) {
int i = left, j = right;
int tmp;
int pivot = arr[(left + right) / 2];
/* partition */
while (i <= j) {
while (arr[i] < pivot)
i++;
while (arr[j] > pivot)
j--;
if (i <= j) {
tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
i++;
j--;
}
};
/* recursion */
if (left < j)
quickSort(arr, left, j);
if (i < right)
quickSort(arr, i, right);
}
ANALYSIS
The best-case behavior of the quicksort algorithm occurs when in each recursion step the partitioning produces two parts of equal length. In order to sort n elements, in this case the running time is in Θ(n log(n)). This is because the recursion depth is log(n) and on each level there are n elements to be treated (Figure 2 a).
The worst case occurs when in each recursion step an unbalanced partitioning is produced, namely that one part consists of only one element and the other part consists of the rest of the elements (Figure 2 c). Then the recursion depth is n-1 and quicksort runs in time Θ(n2).
In the average case a partitioning as shown in Figure 2 b is to be expected.
The choice of the comparison element x determines which partition is achieved. Suppose that the first element of the sequence is chosen as comparison element. This would lead to the worst case behavior of the algorithm when the sequence is initially sorted. Therefore, it is better to choose the element in the middle of the sequence as comparison element.
Even better would it be to take the n/2-th greatest element of the sequence (the median). Then the optimal partition is achieved. Actually, it is possible to compute the median in linear time [AHU 74]. This variant of quicksort would run in time O(n log(n)) even in the worst case.
However, the beauty of quicksort lies in its simplicity. And it turns out that even in its simple form quicksort runs in O(n log(n)) on the average. Moreover, the constant hidden in the O-notation is small. Therefore, we trade this for the (rare) worst case behavior of Θ(n2).
Proposition: The time complexity of quicksort is in
Θ(n log(n)) | in the average case and in | |
Θ(n2) | in the worst case |
BLOGGER:
Shara F. Barcelo
200912035
This entry was posted
on 12:02 AM
and is filed under
Insertion Sort Agorithm vs. Quicksort Algorithm
.
You can leave a response
and follow any responses to this entry through the
Mag-subscribe sa:
I-post ang Mga Komento (Atom)
.